게임 지도에서 최적의 경로 탐색을 위한 개선된 휴리스틱

2006월 6월 20일 제2회 인공지능 및 대화형 디지털 엔터테인먼트 컨퍼런스 발표
게임 지도에서 최적의 경로 탐색을 위한 개선된 휴리스틱 2006년 6월 20일 Improved Heuristics for Optimal Pathfinding on Game Maps https://ojs.aaai.org/index.php/AIIDE/article/view/18740
Abstract
- A* 기반으로 경로 탐색을 안내하는 데 사용되는 휴리스틱 함수는 너무 단순하여 크고 복잡한 게임 세계에서 필요한 패스파인딩을 제공하지 못함
- 크고 복잡한 게임 맵에서 위치 간 거리를 추정하는데에 효과적인 두가지 휴리스틱을 소개
- 데드 엔드 휴리스틱: 현재 쿼리에 적합하지 않은 검색 맵 영역을 제거
- 게이트웨이 휴리스틱: 추정치를 개선하기 위해 게이트웨이를 사용
Introduction
게임 맵이 커지고 복잡해짐에 따라 이러한 단순한 휴리스틱으로는 충분한 목표 안내를 제공할 수 없어 멀리 떨어진 두 맵 위치 사이의 최단 경로를 찾을 때 거의 전체 맵을 탐색하는 경우가 빈번하게 발생한다. 이 문제를 극복하기 위해 사용되는 한 가지 기법은 계층적 경로 찾기. 상위 레이어 중 하나에서 대략적인 경로를 찾은 다음 기본 레이어에서 소규모 로컬 검색을 사용하여 경로를 구체화한다. 이러면 A∗가 더 작은 상태 공간을 탐색하기 때문에 처리 속도가 훨씬 빨라지지만, 반환되는 정보가 최적일 필요가 없다는 점이 단점. 추상화 과정에서 맵의 미세한 디테일 중 일부가 손실되기 때문. 맵에 유닛과 기타 동적 장애물의 수가 증가하면 정확도가 떨어짐. 이 논문에서는 상태 공간 탐색을 줄이면서도 장애물들을 볼 수 있게끔 상태 공간 추상화를 사용해 계층적 보기를 생성하는 대신, 이를 사용해 일반 A∗ 검색을 안내하는 개선된 휴리스틱 함수를 제공. 1) 게임맵에서 경로 찾기 검색을 안내하기 위한 허용 가능한 휴리스틱 측정값 개선 2) 게임맵을 더 작은 영역으로 자동 분해하는 알고리즘 방법
Improved Heuristics

이 지도에서 멀리 떨어진 두 위치 사이의 최단 경로를 찾을 때 옥타일 거리에 기반한 순진한 휴리스틱은 지도의 모든 위치를 탐색할 것. 원하는 목적지로 가는 지름길로 연결되는 경로가 존재하는지 미리 알 수 없기 때문이다. 이 논문에서 제시하는 두 가지 휴리스틱의 기본개념: 주어진 두 위치 사이에서 최적의 경로가 될 수 없는 모든 영역(이 경우에는 회의실)을 미리 식별하고 제외함으로써 이 문제를 완화하는 것
- 데드 엔드 휴리스틱: 막다른 골목으로 이어지는 영역을 피한다
- 게이트웨이 휴리스틱: 특정 방을 통과하면 최적 경로가 아닌 경로로만 이동할 수 있음을 인식
휴리스틱을 계산하는 과정
- 1단계: 맵이 전처리되고 추상 뷰가 생성, 오프라인에서 각 맵에 대해 한 번만 수행 (지도를 더 작은 영역으로 자동 분해한 다음 경로 정보를 계산하는 방식)
- 2단계: 전처리 단계의 추상 뷰를 사용하여 경로 찾기 검색을 위한 개선된 휴리스틱 추정치를 도출
Dead-End Heuristic
막다른 골목으로 이어지는 방, 즉 현재 이 방에서 목표에 이르는 경로가 없는 경우(들어온 입구를 통해 다시 나가는 것 제외)에는 이를 바로 알 수 있다.
Preprocessing Phase

- 1단계: 게임 맵을 여러 개의 작은 영역으로 분해
- 2단계: 여러 영역과 영역 간의 상호 연결을 표현하기 위한 상위 수준 그래프를 구성 그래프의 노드는 영역을 나타내고 노드 사이의 에지는 두 해당 영역 사이의 입구
Runtime Phase
- 멀티그래프에서 탐색 (멀티그래프: 맵의 여러구역이 노드로 표현된 그래프)
- 출발지와 목적지 구역 사이에 있는 관련 구역만 찾아내고 나머지는 막다른 길
- DFS(깊이우선탐색)을 사용해 관련 구역을 찾는다
- 출발지와 목적지 사이의 모든 가능한 경로를 찾기 위해 DFS 사용
- 이미 탐색한 길은 기록해둔다
- 관련 구역만 남기고 나머지는 배제
단점
- 맵의 구조에 의해 크게 좌우됨
- 만약 새로운 경로가 열리면 휴리스틱이 불필요한 구역을 배제하는 데 한계가 생김
- 다양한 경로가 존재하는 맵이면 효과가 적다.
- 구역을 너무 작게 나누면 멀티그래프가 커지고 탐색하는 데 시간이 오래 걸림
- 구역별로 필요한 계산을 해둠으로써 해결할 수 있지만, 그만큼 메모리 사용량이 늘어남
Gateway Heuristic
영역의 입구/출구 사이의 거리를 미리 계산한다.
Preprocessing Phase
- 이 작업은 미리 오프라인(Preprocessing)에서 수행
경로 탐색 속도에 영향을 주지 않고 빠르게 탐색할 수 있지만, 메모리 사용량은 늘어날 수 있음
- 맵을 여러 구역으로 나눈 후, 각 구역 사이의 경계를 게이트(Gate)라고 정의 게이트는 맵의 구역을 연결하는 입구나 출구 (방에서 복도로 나가는 문이나, 복도 끝에 있는 통로 등)
게이트는 수평이나 수직 방향으로 설정
- 이 때, 한 게이트에서 출발해 다른 게이트에 도착할 때까지의 거리를 기록
- 각 게이트에서 다른 게이트까지의 최단 경로를 여러 번의 A* 탐색을 통해 계산
- 중요한 점은 게이트 간의 경로를 2방향으로 따로 계산한다는 것
- 게이트 출발과 도착의 각 가능성에 대해 별도의 거리를 알고 싶기 때문
- 출발지 게이트에서 도착지 게이트로 가는 경로와 그 반대 경로를 각각 계산
- 하나의 비용 값만 계산할 때보다 런타임 중에 훨씬 더 정확한 휴리스틱 추정치를 얻을 수 있다
- 각 게이트 간에는 4가지 비용이 저장됨
- 예를 들어, 방 A에서 방 B로 가는 경로와 방 B에서 방 A로 돌아가는 경로는 다를 수 있으므로, 방향을 고려한 경로 계산이 이루어짐
Runtime Phase
런타임 단계는 아래의 휴리스틱 함수를 사용하는 일반 A* 검색 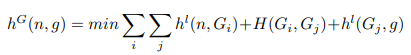
A* 알고리즘은 게이트 간 미리 계산된 거리 정보를 활용하여 경로 탐색을 진행
- hG(n,g): 출발점 n에서 목표점 g까지의 거리를 추정한 결과값
- hl(n,Gi): 현재위치 n에서 가장 가까운게이트 Gi까지의 거리
- H(Gi,Gj): 게이트Gi와 게이트Gj 사이의 미리 계산된 최단 거리
- hl(Gj,g): 목표 위치 g에서 가장 가까운 게이트 Gj까지의 거리
이 함수를 통해 모든 게이트 조합을 계산하여, 출발지와 목표지 사이에서 최단 경로를 제공하는 게이트들을 찾는다.
- 모든 게이트 쌍 Gi와 Gj의 경로를 비교한 후, 가장 짧은 경로를 선택
- 모든 가능한 게이트 경로 중에서 가장 짧은 경로를 선택
단점
- 게이트의 크기가 클수록 경로 탐색에서 약간의 오류가 발생할 수 있음
- 출발지에서 게이트까지의 거리나 도착지에서 게이트까지의 거리 계산이 조금 부정확해질 수 있기 때문
- 일반적으로 이러한 오차는 크지 않음
Decomposition Algorithm
맵을 여러 개의 작은 구역으로 자동으로 나누는 방법을 설명하는 파트
의사코드
Automatic Map Decomposition
# 맵의 모든 타일을 '통과 가능(free)'으로 초기화
for 모든 맵 타일:
zone(tile) = 'free'
end for
# 현재 구역 번호를 1로 시작
currZone = 1
# 반복적으로 구역을 생성
repeat:
# 아직 구역이 할당되지 않은 가장 왼쪽 위의 통과 가능한 타일을 찾음
(xLeft, y) = 맵에서 가장 위쪽의 왼쪽 타일 중 'free(통과가능)'한 타일을 찾음
# 오른쪽과 왼쪽 경계가 줄어들었는지 체크할 변수 초기화
shrunkR = False
shrunkL = False
repeat:
# 현재 라인의 타일을 벽이나 이미 할당된 구역을 만날 때까지 오른쪽으로 채움
x = xLeft
zone(x, y) = currZone
while (x + 1, y)가 'free'이고 (x + 1, y - 1)가 '!free'일 때까지:
x = x + 1
zone(x, y) = currZone
end while
# 만약 오른쪽 경계가 줄어들었다가 다시 커지면, 구역 채우기를 멈춤
if (x + 1, y - 1) == currZone:
shrunkR = True
# (x, y - 1)가 현재 구역이 아니고 줄어든 오른쪽이라면:
else if (x, y - 1) != currZone && (x, y - 1) == shrunkR:
# 이미 채운 라인을 되돌림
while (x, y) == currZone:
Zone(x, y) = 'free'
x = x - 1
end while
break
end if
# 다음 줄로 이동, 같은 x 위치에서 시작
(x, y) = (xLeft, y + 1)
# 장애물이 있으면 구역 내부에서 오른쪽으로 이동
while (x, y) != 'free' && zone(x, y - 1) == currZone:
x = x + 1
end while
# 왼쪽으로 이동하며 구역 경계 설정
while (x - 1, y) == 'free' && (x - 1, y - 1) != 'free':
x = x - 1
end while
# 만약 왼쪽 경계가 줄어들었다가 다시 커지면, 구역 채우기를 멈춤
if (x - 1, y - 1) == currZone:
shrunkL = True
else if (x, y - 1) != currZone && (x, y - 1) == :
break # 채우기 중단
end if
until break # 구역을 다 채울 때까지 반복
# 다음 구역 번호로 이동
currZone = currZone + 1
until 맵에서 더 이상 통과 가능한 타일이 없을 때까지 반복
초기화
- 맵의 모든 타일을 “통과 가능” 상태로 설정
- 첫 번째 구역부터 시작하며, 구역 번호는 1로 설정됨
구역 채우기
- 맵에서 가장 왼쪽 위에 있는 통과 가능한 타일을 찾음
- 이 타일을 시작점으로 새로운 구역을 생성
- 줄 단위로 타일을 오른쪽으로 이동하며, 벽이나 다른 구역을 만날 때까지 구역을 채워나감.
경계가 커지거나 줄어드는지 확인
- 구역을 채우는 과정에서, 오른쪽과 왼쪽 경계가 커지거나 줄어드는지 확인
- 만약 구역의 경계가 줄어들었다가 다시 커지면, 구역 채우기를 멈추고 현재 구역을 종료
다음줄로 이동
- 한 줄을 다 채웠으면 아래 줄로 이동하여 다시 채우기를 시작
- 이때, 왼쪽 경계부터 오른쪽으로 이동하며 채워나감
구역이 다 채워지면 다음 구역으로 이동
- 하나의 구역이 다 채워지면, 맵에서 남은 통과 가능한 타일을 찾아서 새로운 구역 시작
- 맵의 모든 타일이 할당될 때까지 반복

그림 4는 분해 알고리즘이 어떻게 작동하는지 보여주는 예시
- 왼쪽 위 이미지는 분할되지 않은 맵
- 오른쪽 위 이미지는 알고리즘이 시작된 상태
- 4번째줄이 위쪽으로 열려있기 때문에 중지되었음 ((x + 1, y − 1) != free 조건에 걸림)
- 왼쪽 아래 이미지는 구역 채우기를 완료한 상태
- 마지막 이미지에선 다음 영역 채우기를 시작한 상태
Empirical Evaluation
평가시작.
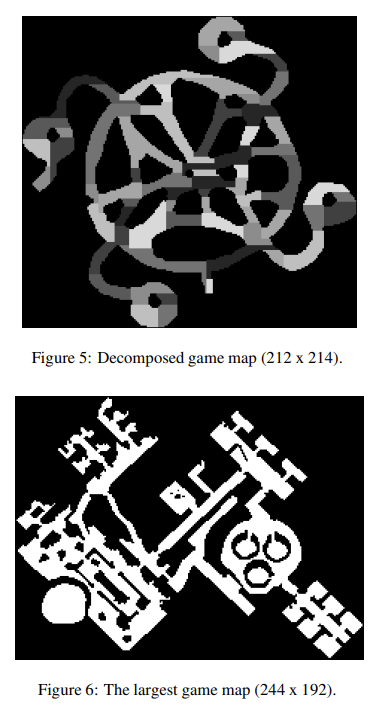
테스트맵은 데모맵과 ‘발더스게이트2’에서 가져온 맵으로 실험한다.
- 각 맵에 대해 1000번의 경로 탐색을 무작위 시작과 목표지점으로 실행
- 논문에서 기술한 휴리스틱과 기존의 옥타일 휴리스틱을 비교 분석
- 탐색에 필요한 노드의 수와 총 실행시간을 기록 (노드 수가 적고 실행 시간이 짧을수록 휴리스틱이 더 효율적인 것)
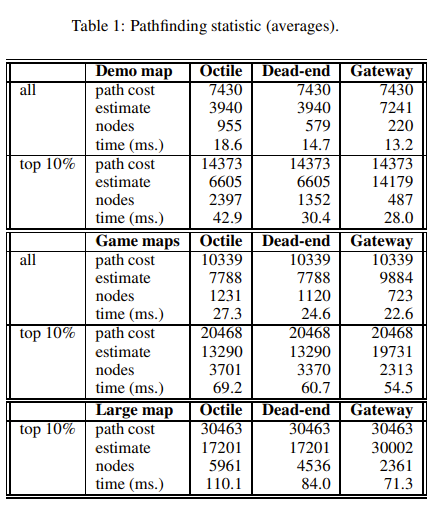
결과를 아래의 표로 정리했다. 옥타일 휴리스틱과 비교한 표.
 Octile Heuristic: 일반적으로 그리드 기반 맵에서 사용되는 간단한 휴리스틱
Octile Heuristic: 일반적으로 그리드 기반 맵에서 사용되는 간단한 휴리스틱
- Dead-end 휴리스틱과 Gateway 휴리스틱 모두 기존의 옥타일 휴리스틱보다 더 적은 노드를 확장하고 더 짧은 시간에 경로를 찾아냄
- Gateway 휴리스틱은 모든 맵 유형에서 노드 수의 감소와 실행 시간의 단축 모두 가장 우수한 성능을 보임
Conclusions
- Dead-End 휴리스틱과 Gateway 휴리스틱 모두 탐색할 때 확장해야 하는 노드 수를 크게 줄였고, 결과적으로 탐색 시간을 단축
- 향후 연구에서 휴리스틱의 정확성을 더 높이는 방법과, 맵 분할 알고리즘을 다양한 지형 유형에 맞게 최적화하는 방법을 탐구할 필요성이 있음
